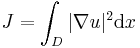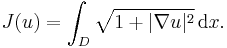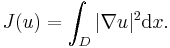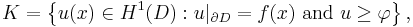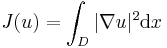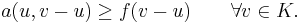Obstacle problem
The obstacle problem is a classic motivating example in the mathematical study of variational inequalities and free boundary problems. The problem is to find the equilibrium position of an elastic membrane whose boundary is held fixed, and which is constrained to lie above a given obstacle. It is deeply related to the study of minimal surfaces and the capacity of a set in potential theory as well. Applications include the study of fluid filtration in porous media, constrained heating, elasto-plasticity, optimal control, and financial mathematics.[1]
The mathematical formulation of the problem is to seek minimizers of the Dirichlet energy functional,
in some domain  where the functions
where the functions  represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions
represent the vertical displacement of the membrane. In addition to satisfying Dirichlet boundary conditions corresponding to the fixed boundary of the membrane, the functions  are in addition constrained to be greater than some given obstacle function
are in addition constrained to be greater than some given obstacle function 
 . The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.
. The solution breaks down into a region where the solution is equal to the obstacle function, known as the contact set, and a region where the solution is above the obstacle. The interface between the two regions is the free boundary.
In general, the solution is continuous and possesses Lipschitz continuous first derivatives, but that the solution is generally discontinuous in the second derivatives across the free boundary. The free boundary is characterized as a Hölder continuous surface except at certain singular points, which reside on a smooth manifold.
Contents |
Motivating problems
Shape of a membrane above an obstacle
The obstacle problem arises when one considers the shape taken by a soap film in a domain whose boundary position is fixed (see Plateau's problem), with the added constraint that the membrane is constrained to lie above some obstacle 
 in the interior of the domain as well.[2] In this case, the energy functional to be minimized is the surface area integral, or
in the interior of the domain as well.[2] In this case, the energy functional to be minimized is the surface area integral, or
This problem can be linearized in the case of small perturbations by expanding the energy functional in terms of its Taylor series and taking the first term only, in which case the energy to be minimized is the standard Dirichlet energy
Optimal stopping
The obstacle problem also arises in control theory, specifically the question of finding the optimal stopping time for a stochastic process with payoff function 
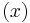 .
.
In the simple case where the process is Brownian motion, and the process is forced to stop upon exiting the domain, the solution 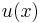 of the obstacle problem can be characterized as the expected value of the payoff, starting the process at
of the obstacle problem can be characterized as the expected value of the payoff, starting the process at  , if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.[3]
, if the optimal stopping strategy is followed. The stopping criterion is simply that one should stop upon reaching the contact set.[3]
Formal statement
Suppose the following data is given:
- an open bounded domain
 ⊂ ℝn with smooth boundary
⊂ ℝn with smooth boundary - a smooth function
 on ∂
on ∂ (the boundary of
(the boundary of  )
) - a smooth function

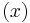 defined on all of
defined on all of  such that
such that 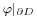 <
<  , i.e. the restriction of
, i.e. the restriction of 
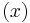 to the boundary of
to the boundary of  (its trace) is less than
(its trace) is less than  .
.
Then consider the set
which is a closed convex subset of the Sobolev space of square integrable functions with square integrable weak first derivatives, containing precisely those functions with the desired boundary conditions which are also above the obstacle. The solution to the obstacle problem is the function which minimizes the energy integral
over all functions 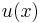 belonging to
belonging to  ; the existence of such a minimizer is assured by considerations of Hilbert space theory.[2][4]
; the existence of such a minimizer is assured by considerations of Hilbert space theory.[2][4]
Alternative formulations
Variational inequality
The obstacle problem can be reformulated as a standard problem in the theory of variational inequalities on Hilbert spaces. Seeking the energy minimizer in the set  of suitable functions is equivalent to seeking
of suitable functions is equivalent to seeking
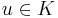 such that
such that 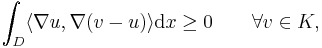
where ⟨ . , . ⟩ : ℝn × ℝn → ℝ is the ordinary scalar product in the finite dimensional real vector space ℝn. This is a special case of the more general form for variational inequalities on Hilbert spaces, whose solutions are functions  in some closed convex subset
in some closed convex subset  of the overall space, such that
of the overall space, such that
for coercive, real-valued, bounded bilinear forms 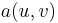 and bounded linear functionals
and bounded linear functionals 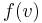 .[5]
.[5]
Least superharmonic function
A variational argument shows that, away from the contact set, the solution to the obstacle problem is harmonic. A similar argument which restricts itself to variations that are positive shows that the solution is superharmonic on the contact set. Together, the two arguments imply that the solution is a superharmonic function.[1]
In fact, an application of the maximum principle then shows that the solution to the obstacle problem is the least superharmonic function in the set of admissible functions.[5]
Regularity properties
Optimal regularity
The solution to the obstacle problem has 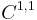 regularity, or bounded second derivatives, when the obstacle itself has these properties.[6] More precisely, the solution's modulus of continuity and the modulus of continuity for its derivative are related to those of the obstacle.
regularity, or bounded second derivatives, when the obstacle itself has these properties.[6] More precisely, the solution's modulus of continuity and the modulus of continuity for its derivative are related to those of the obstacle.
- If the obstacle
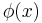 has modulus of continuity
has modulus of continuity 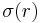 , that is to say that
, that is to say that 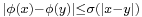 , then the solution
, then the solution 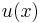 has modulus of continuity given by
has modulus of continuity given by 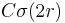 , where the constant depends only on the domain and not the obstacle.
, where the constant depends only on the domain and not the obstacle. - If the obstacle's first derivative has modulus of continuity
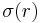 , then the solution's first derivative has modulus of continuity given by
, then the solution's first derivative has modulus of continuity given by 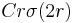 , where the constant again depends only on the domain.[7]
, where the constant again depends only on the domain.[7]
Level surfaces and the free boundary
Subject to a degeneracy condition, level sets of the difference between the solution and the obstacle, 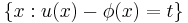 for
for 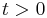 are
are 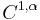 surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also
surfaces. The free boundary, which is the boundary of the set where the solution meets the obstacle, is also 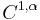 except on a set of singular points, which are themselves either isolated or locally contained on a
except on a set of singular points, which are themselves either isolated or locally contained on a 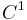 manifold.[8]
manifold.[8]
Generalizations
The theory of the obstacle problem is extended to other divergence form uniformly elliptic operators,[5] and their associated energy functionals. It can be generalized to degenerate elliptic operators as well.
The double obstacle problem, where the function is constrained to lie above one obstacle function and below another, is also of interest.
The Signorini problem is a variant of the obstacle problem, where the energy functional is minimized subject to a constraint which only lives on a surface of one lesser dimension, which includes the boundary obstacle problem, where the constraint operates on the boundary of the domain.
The parabolic, time-dependent cases of the obstacle problem and its variants are also objects of study.
See also
Notes
- ^ a b See Caffarelli 1998, p. 384.
- ^ a b See Caffarelli 1998, p. 383.
- ^ See the lecture notes by Evans (Version 1.2, pp. 110–114).
- ^ See Kinderlehrer & Stampacchia 1980, pp. 40–41.
- ^ a b c See Kinderlehrer & Stampacchia 1980, pp. 23–49.
- ^ See Frehse 1972.
- ^ See Caffarelli 1998, p. 386.
- ^ See Caffarelli 1998, p. 394 and 397.
References
- Caffarelli, Luis (July 1998), "The obstacle problem revisited", The Journal of Fourier Analysis and Applications 4 (4-5): 383–402, doi:10.1007/BF02498216, MR1658612, Zbl 0928.49030, http://www.springerlink.com/content/u2105854886n6282/
- Evans, Lawrence (Version 1.2), An Introduction to Stochastic Differential Equations, pp. 130, http://math.berkeley.edu/~evans/SDE.course.pdf, retrieved July 11, 2011. A set of lecture notes surveying "without too many precise details, the basic theory of probability, random differential equations and some applications", as the author himself states.
- Frehse, Jens (1972), "On the regularity of the solution of a second order variational inequality", Bolletino della Unione Matematica Italiana, Serie IV, 6: 312–215, MR318650, Zbl 0261.49021.
- Friedman, Avner (1982), Variational principles and free boundary problems, Pure and Applied Mathematics, New York: John Wiley & Sons, pp. ix+710, ISBN 0-471-86849-3, MR0679313, Zbl 0564.49002.
- Kinderlehrer, David; Stampacchia, Guido (1980), An Introduction to Variational Inequalities and Their Applications, Pure and Applied Mathematics, 88, New York: Academic Press, pp. xiv+313, ISBN 0-12-407350-6, MR0567696, Zbl 0457.35001
External links
- Caffarelli, Luis (August 1998), The Obstacle Problem, draft from the Fermi Lectures, pp. 45, http://www.ma.utexas.edu/users/combs/obstacle-long.pdf, retrieved July 11, 2011, delivered by the author at the Scuola Normale Superiore in 1998.